Du kender det helt sikkert, når du bruger GA4 – du har 20% demgrafisk data til rådighed, når du arbejder med fx dine brugeres adfærd i forhold til køn. Denne artikel fokuserer på, hvordan du kan udregne konfidensintervallet, som kan fortælle dig, hvor valid din data
Flere typer af validitet
Når du skal udregne validiteten på en stikprøve, bliver du nødt til at vurdere, hvor godt stikprøven repræsenterer den samlede population, og hvor præcist de målte resultater afspejler de sande værdier i populationen.
Validitet kan opdeles i flere typer, herunder intern og ekstern validitet, men vi vil her fokusere på generelle metoder og overvejelser ved beregning af validitet i stikprøveudtagning.
Typer af Validitet
1. Intern Validitet: Henviser til i hvilken grad de opnåede resultater er korrekte for den specifikke stikprøve. Det betyder, at undersøgelsen er fri for systematiske fejl, og at resultaterne faktisk er forårsaget af de undersøgte variable og ikke af andre faktorer.
2. Ekstern Validitet: Handler om i hvor høj grad resultaterne fra stikprøven kan generaliseres til den bredere population. Dette afhænger af stikprøvens repræsentativitet.
Faktorer der Påvirker Validiteten
1. Stikprøvens størrelse: En større stikprøve giver generelt mere præcise estimater og højere validitet, fordi den bedre repræsenterer populationen.
2. Stikprøveudtagning: Metoden for udvælgelse af stikprøven er afgørende. Tilfældig udvælgelse (random sampling) er ideel, da det reducerer bias og sikrer, at hver enhed i populationen har en lige stor chance for at blive inkluderet.
3. Måleinstrumenternes pålidelighed: Måleinstrumenter (GA4) skal være pålideligt (reliable) og gyldige (valid) for at sikre, at de faktisk måler det, de påstår at måle. Som du helt sikkert ved, så er GA4 et af de mere pålidelige tools, vi arbejder med, men der er stadig cookie consent, cookie levetid og mange, mange flere bias.
Beregning af Validitet
Konfidensinterval
En måde at vurdere stikprøvens validitet på er at beregne konfidensintervaller.
Konfidensintervallet giver et interval af værdier, som med en vis sandsynlighed indeholder populationens sande parameter (validitet).
Formlen for konfidensinterval for en populationsmiddelværdi er:
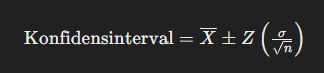
Konfidensintervallet (CI) for en stikprøve kan beregnes, uanset stikprøvens andel af populationen. Når stikprøven udgør 20 % af populationen, påvirkes beregningen af konfidensintervallet af den endelige populationskorrektion (finite population correction, FPC), hvis populationen er forholdsvis lille. Hvis populationen er meget stor, kan vi ofte se bort fra FPC.
Lad os tage udgangspunkt i følgende scenarie for at illustrere, hvordan man beregner konfidensintervallet, når stikprøven er 20 % af populationen.
Eksempel
– Populationens størrelse (N) = 10000
– Stikprøvens størrelse (n) = 2000 (20 % af 10000)
– Stikprøvens gennemsnit (X) = 50
– Stikprøvens standardafvigelse (s) = 10
– Konfidensniveau = 95 % (Z-værdi = 1.96)
Trin 1: Beregning af Standard Error (SE)

Trin 2: Anvendelse af Finite Population Correction (FPC)
FPC bruges, når stikprøven er en betydelig del af populationen (typisk når \(n\) er mere end 5 % af \(N\)).
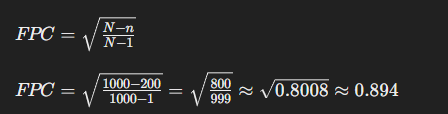
Trin 3: Justeret Standard Error med FPC
Justere standard error ved at multiplicere med FPC:
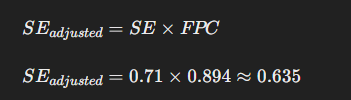
Trin 4: Beregning af Konfidensintervallet
Konfidensintervallet beregnes som:

Dette betyder, at vi med 95 % sikkerhed kan sige, at den sande gennemsnitsværdi for populationen ligger mellem 48.755 og 51.245.
For at kunne forstå disse to tal, bliver vi nødt til at kigge nærmere på, hvordan vi forstår konfidensintervaller.
Forståelse af Konfidensinterval
Konfidensintervallet, som vi beregnede, giver et interval af værdier, som med en vis sandsynlighed indeholder den sande populationsparameter (i dette tilfælde gennemsnittet) baseret på vores stikprøvedata. Lad os dykke dybere ned i betydningen af de beregnede værdier 48,755 og 51,245 i konteksten af konfidensintervallet.
1. Definition af Konfidensinterval: Et konfidensinterval er et intervalestimat, der sandsynligvis indeholder populationsparameteren. Konfidensintervallet gives ved to tal, der afgrænser et interval: nedre grænse og øvre grænse.
2. Betydning af Konfidensniveau: Konfidensniveauet (ofte 95 %) angiver, hvor sikker vi er på, at intervallet indeholder den sande parameter. Et 95 % konfidensinterval betyder, at hvis vi gentager prøvetagningen mange gange, vil 95 % af de beregnede konfidensintervaller indeholde den sande populationsparameter.
Hvad betyder de specifikke værdier: 48,755 og 51,245?
Nedre Grænse (48,755): Dette tal repræsenterer den laveste værdi, som vi med 95 % sikkerhed tror, at populationsgennemsnittet kunne være, givet vores stikprøvedata. Det betyder, at der er en meget lille sandsynlighed (5 % i alt, men 2,5 % i hver ende af normalfordelingskurven) for, at det sande gennemsnit er mindre end 48,755.
Øvre Grænse (51,245): Dette tal repræsenterer den højeste værdi, som vi med 95 % sikkerhed tror, at populationsgennemsnittet kunne være, givet vores stikprøvedata. Det betyder, at der er en meget lille sandsynlighed for, at det sande gennemsnit er højere end 51,245.
Hvordan Fortolkes Disse Værdier?
Lad os sige, at vi undersøgte den gennemsnitlige kønsfordeling på en konto og fandt, at stikprøvens gennemsnit var 20% med et 95 % konfidensinterval på [48,755, 51,245].
Repræsentativitet og Præcision: Intervallet [48,755, 51,245] giver os en rækkevidde, inden for hvilken vi er ret sikre på, at den sande gennemsnitlige højde af alle mænd i byen falder. Jo snævrere intervallet er, desto mere præcist er vores estimat.
Konfidensniveau: Hvis vi skulle tage mange stikprøver fra populationen og beregne konfidensintervallet for hver stikprøve, ville cirka 95 % af disse intervaller indeholde det sande gennemsnit af populationen. Dette betyder ikke, at 95 % af værdierne i populationen falder inden for intervallet, men snarere at 95 % af de intervaller, vi beregner, vil ramme den sande populationsparameter.
Brug i Beslutningstagning
Konfidensintervallet kan anvendes til at vurdere, hvor præcist stikprøvens gennemsnit reflekterer populationens gennemsnit og til at træffe informerede beslutninger:
Evaluering af Usikkerhed: Det giver en kvantificering af usikkerheden omkring stikprøveestimaterne. Hvis vi havde et meget bredt konfidensinterval, ville det indikere stor usikkerhed omkring estimatet, mens et smalt interval indikerer større præcision.
Sammenligning med Andre Data: Vi kan sammenligne konfidensintervallet med andre data eller benchmarks for at vurdere forskelle eller ligheder. Hvis et andet dataset for gennemsnitshøjden i en anden by ligger uden for dette interval, kan det indikere en signifikant forskel mellem de to byer.
De specifikke værdier 48,755 og 51,245 i konfidensintervallet repræsenterer de nedre og øvre grænser for vores intervalestimat af populationsgennemsnittet. Med 95 % sikkerhed kan vi sige, at det sande gennemsnit ligger inden for dette interval baseret på vores stikprøve. Dette interval hjælper med at forstå præcisionen af vores estimater og graden af usikkerhed forbundet med stikprøvedataene.

